blog.amartynov.ru

Долгое время меня беспокоил вопрос, почему слова “интерполяция” и “фильтр” порой употребляются как взаимозаменяемые. Например, билинейная фильтрация и билинейная интерполяция по сути одно и то же явление.

Несколько лет назад я уже пытался в этом разобраться в контексте статьи про сэмплирование, квантование, фильтры и интерполяцию. Статья получилась так себе — я в ней налажал и ничего толком не объяснил, потому что разобраться в такой теме с наскоку невозможно. Теперь по прошествии нескольких лет я поумнел и, кажется, вник в суть.

Поехали. Я буду считать, что вы знаете, чем дискретный сигнал отличается от непрерывного, и зачем вообще всё это нужно.

Возьмем 6 дискретных отсчетов:

Для простоты (но, как говорится, не теряя общности) предположим, что интервал семплирования равен 1 (то есть отсчеты взяты в “целые моменты времени”):

Если надо получить непрерывный сигнал, проходящий через эти точки, то самое простое и интуитивно понятное из возможного — это соединить их прямыми линиями:

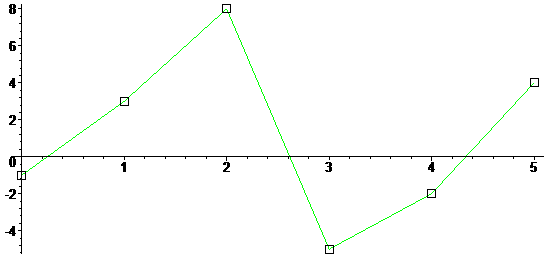
Это, собственно, и есть линейная интерполяция. Кто в теме, тот может предложить еще сплайны, sinc-ряд и, возможно, еще какие-то методы, но мы сейчас будем заниматься не этим.

Давайте представим линейную интерполяцию немножко по-другому. Вместо того, чтобы соединять точки линиями, мы в каждый отчет поместим по вот такому “треугольничку”:

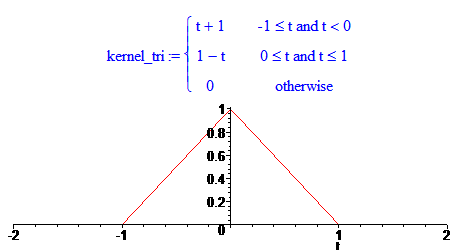
Говоря “поместим”, я имею в виду, что мы сдвинем его в позицию дискретного отсчета и умножим на его значение:

В результате получится вот такая кусочно-линейная функция:

А её график мы уже где-то видели:

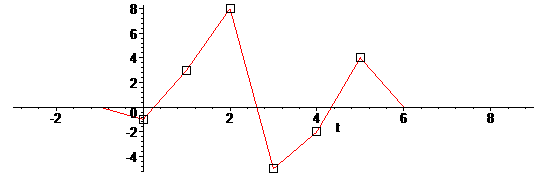
Вот процесс в действии:

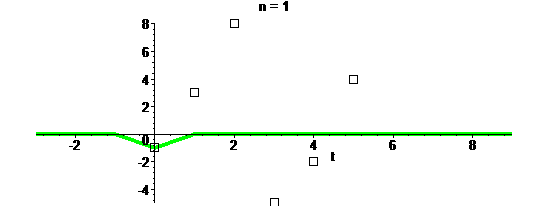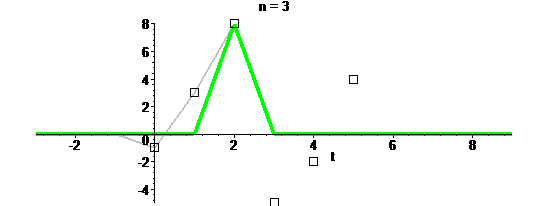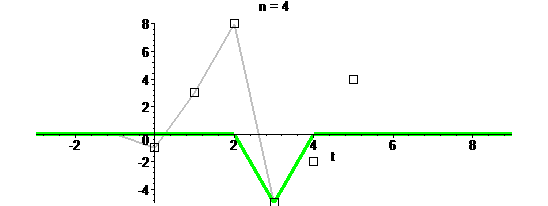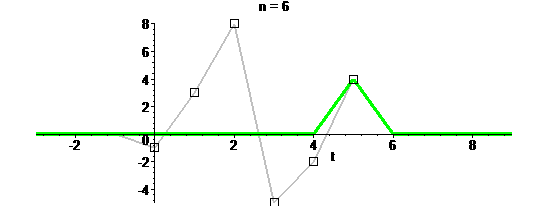
На каждом шаге к “серой” функции прибавляется зеленый треугольник.

Треугольник называется ядром интерполяции (interpolation kernel) или попросту интерполятором.

Можно применять разные ядра. Например, квадратное:

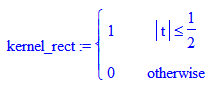
Оно самое простое и в математическом плане, и для визуального восприятия:

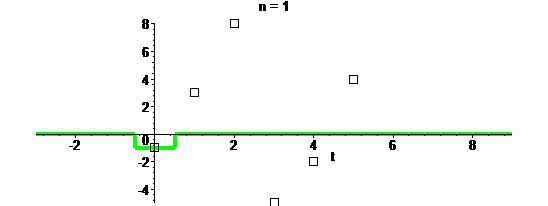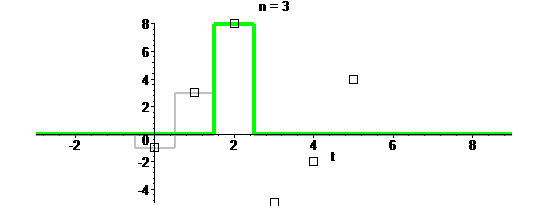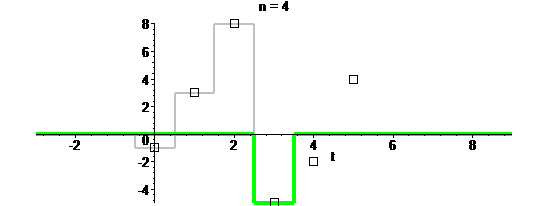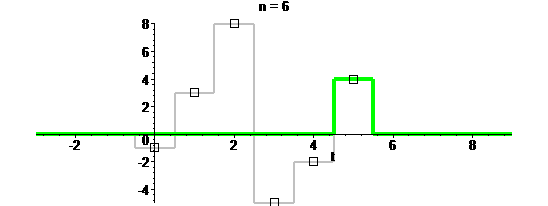
Один минус: пушку таким ядром не зарядишь.

Те, кто знаком с теоремой Котельникова, знают об интерполяции с помощью sinc-функций:

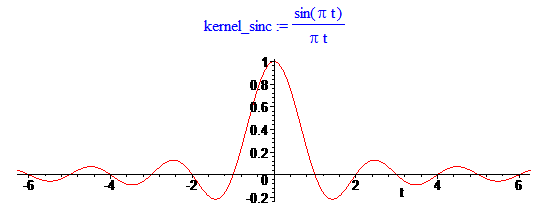
Такая интерполяция дает максимально гладкий сигнал с финитным спектром, но бесконечный во временной области (данный вопрос я обсуждаю в отдельной статье):

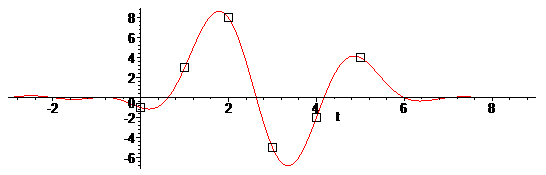
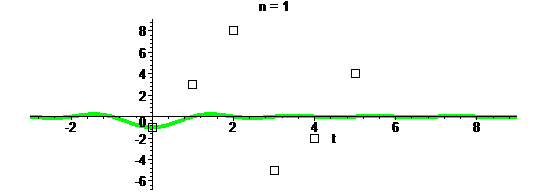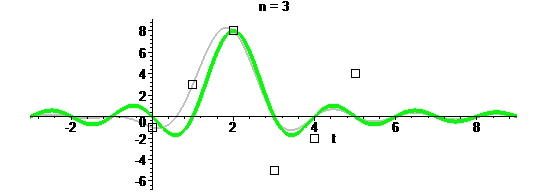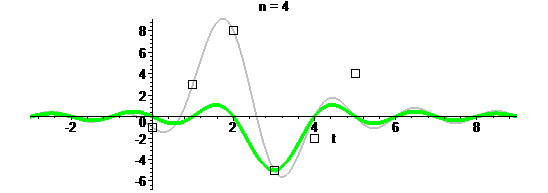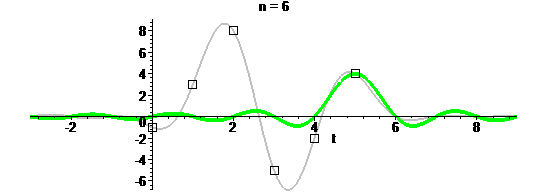
Надеюсь, после нескольких примеров стало хорошо понятно, как работает такая интерполяция. Осталось узнать, как сей процесс называется. А называется он сверткой дискретной последовательности с непрерывной функцией. По-английски convolution.

Я раньше сам долго не мог врубиться, что такое свертка. Определения в духе “схожесть одной функции с отражённой и сдвинутой копией другой” совсем не помогали. А вот ее применение для интерполяции мне показалось очень понятным и доходчивым: одна функция бежит вдоль всех возможных значений другой, и результат суммируется.

Одно из основных применений свертки в теории цифровых сигналов — это фильтрация. Получается, что в основе интерполяции и фильтрации лежит один и тот же математический инструмент.

Недавно я изучал Digital Signal Processing на Coursera. Там был форум, и представилась возможность пообщаться со специалистами из EPFL. Я задал вопрос:

When I look at the following two expressions [digital filtering and interpolation], I see that actually they do the same thing: some “template” (filter’s impulse response or interpolation kernel) is shifted along the time “axis” and scaled by the signal samples. Their cumulative sum forms the result. Do they both represent the same phenomenon described slightly differently (one discrete, other continuous)?

То есть я спросил, являются ли фильтрация и интерполяция одним и тем же явлением. Мне ответил Robin Scheibler:

Both of them are convolutions. [Second expression] is the convolution of a discrete signal with a continuous signal. Often, this is how interpolation can be described, where the discrete signal is the signal to interpolate and the continuous signal is the interpolation filter (e.g. sinc, rect, splines, etc).

Оказывается, интерполирующая функция (которая ядро) имеет полное право называться интерполирующим фильтром.

Я не даром выделил слово “often” (часто). Дело в том, что не каждая интерполяция может быть выражена через свертку.

Яркий пример — это интерполяция кубическими сплайнами. На каждом отрезке между соседними дискретными отсчетами необходимо оценивать значения производных, или, иначе говоря, наклон касательных на концах. Как видно из примера ниже, эти наклоны всегда разные, а значит общего ядра нет.

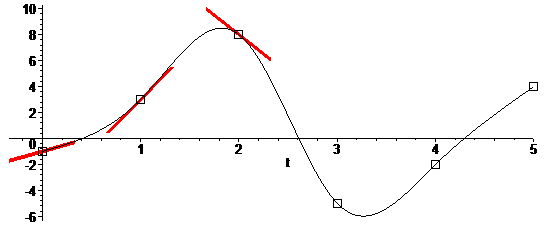
Можно, конечно, выбрать одинаковые “нейтральные” условия в виде равенства производной нулю:

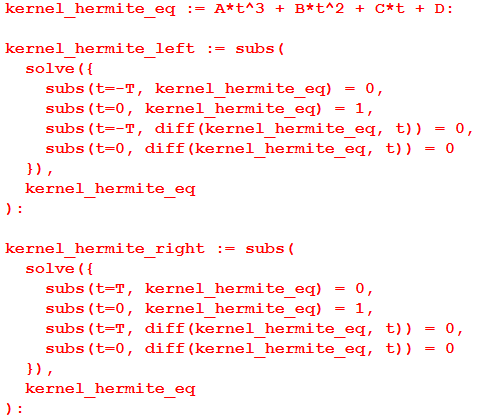
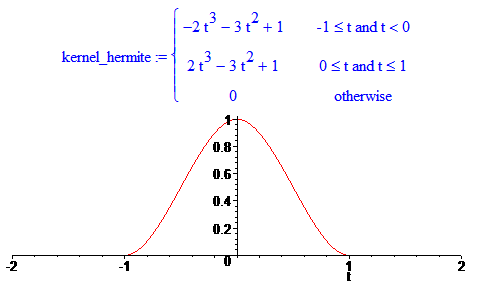
Выглядит “колокольчик” хорошо, но результаты интерполяции с помощью него не слишком впечатляют:

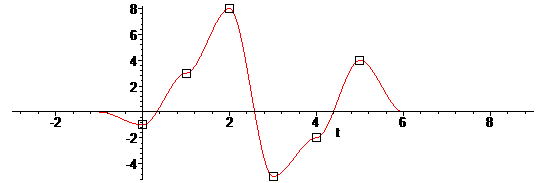
В пиках все нормально, а в точках монотонного роста возникли некрасивые перегибы.

Тем не менее, существует хороший способ сверточной интерполяции с помощью кубического ядра (ох я и загнул). Его описал Robert G. Keys в своей работе Cubic convolution interpolation for digital image processing (PDF):

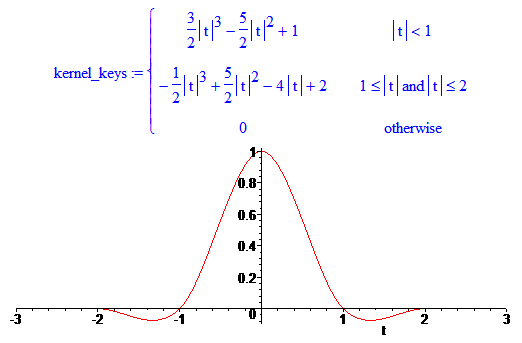
Вот так выглядит результат:

Можно заметить, что из всех рассмотренных ядер, эта “шляпа” больше всех похожа на sinc. Другой распространенный sinc-подобный фильтр (видите, я уже вовсю использую “фильтр”, “ядро” и “интерполятор” как синонимы) — это Lanczos.

Так, кажется это все, что я хотел рассказать.