Фурье-анализ и аддитивный синтез звука струны акустической гитары

17.11.2012

Несмотря на академическое название, тут не будет интегралов и всяких этих “из последней жуткой формулы очевидно”. Тут будет несколько цветастых графиков, немного кода на C# и мои попытки доходчиво объяснить сложные вещи.

О чем пойдет речь

Эта статья — продолжение моего ~~предыдущего эксперимента~~, где я, вооружившись Adobe Audition, разбирал на мелкие запчасти запись звучания моей гитары. Там я все делал на глазок, а теперь хочу с помощью точных расчетов проследить характер звучания нескольких первых гармоник, попробовать их приблизить более-менее простыми функциями и на основании полученных данных синтезировать гитарный звук.

План

С помощью дискретного преобразования Фурье (ДПФ) я соберу статистику об амплитудах гармоник. Обсужу интерпретацию результатов ДПФ.
Используя какую-нибудь интерполяцию приближу закон убывания амплитуд и попробую найти какие-нибудь закономерности. Вдруг они есть?
Аддитивным синтезом сгенерирую звук гитары, и, может быть, даже сыграю им небольшой музыкальный фрагмент.

Исходные данные

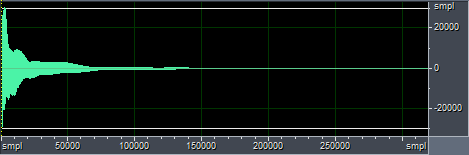
Возьмем тот же звук, который я рассматривал в ~~той статье~~:

На картинке (на нее можно нажать) видно, что звук как бы состоит из нескольких переплетающихся волн. Их-то и предстоит “выщепить”.

Фурье, ДПФ, FFT и т.п.

Если для вас эти слова вообще пустой звук, то можно обратиться к источникам [1] и [8].

Преобразование Фурье переводит осциллограмму в спектрограмму. Как правило, при обработке дискретных сигналов используется быстрое преобразование Фурье (БПФ, Fast Fourier Transform, FFT) — я буду использовать сокращение FFT, оно мне почему-то больше нравится.

FFT принимает на вход PCM-данные, то есть массив значений амплитуды на дискретной сетке. На выходе дает массив такой же длины, но элементами массива являются данные об амплитуде и фазе элементарных синусоид на определенных частотах.

Как я обещал в самом начале, вникать в математические дебри я тут не буду, а просто воспользуюсь библиотекой MathNet.Numerics [2]:

// Read raw pcm file
static IList<short> LoadPcm(string path, long skip, int take) {
    using(var stream = File.OpenRead(path))
    using(var reader = new BinaryReader(stream)) {
        stream.Seek(2 * skip, SeekOrigin.Begin);

        var result = new List<short>(take);
        for(var i = 0; i < take; i++)
            result.Add(reader.ReadInt16());

        return result;
    }
}

static Complex[] CalculateFFT(IList<short> pcm) {
    var complexPcm = pcm.Select(i => (Complex)i).ToArray();
    Transform.FourierForward(complexPcm, FourierOptions.Matlab);
    return complexPcm;
}

Видно, что FFT выдает массив комплексных чисел. И очень важно уметь правильно их интерпретировать.

Первое свойство — этот массив получается симметричным относительно центра. Вторая половина содержит комплексно-сопряженные данные, идущие в обратном порядке, и практического интереса не представляет.

Далее, в FFT-массиве на индексе i содержится информация по частоте

i * SAMPLE_RATE / FFT_SIZE

Например, если исходный сигнал имеет частоту дискретизации 44100, и для анализа мы взяли порцию длиной 4410, то о частоте 220 Гц можно узнать из элемента массива под индексом

i = freq * FFT_SIZE / SAMPLE_RATE

то есть

220 * 4410 / 44100 = 22

Поскольку только половина массива содержит полезные данные, в FFT нет информации о частотах выше SAMPLE_RATE / 2, что хорошо известно из теоремы Котельникова [5].

Какую именно информацию несут комплексные числа в этом массиве? Информацию об амплитуде и фазе. Амплитуда получается, если умножить модуль комплексного числа (по-английски называемый magnitude) на правильный нормировочный множитель (об этом чуть ниже), а фаза — из выражения

arg(FFT[i]) = atan2(Im(FFT[i], Re(FFT[i]))

Насчет правильного нормировочного множителя. Формулы FFT-преобразования бывают разными:

The normalization factor multiplying the DFT and IDFT and the signs of the exponents are merely conventions, and differ in some treatments [4]

Если использовать формулы, принятые в Matlab (обратите внимание на FourierOptions.Matlab в коде функции CalculateFFT выше), то множитель будет 2 / FFT_SIZE (утверждается в [3]):

Amplitude_at_freq = | FFT[i] | * 2 / FFT_SIZE

На C#:

static int IndexForFreq(Complex[] fft, double freq) {
    return Convert.ToInt32(freq * fft.Length / SAMPLE_RATE);
}

static double AmplitudeFromFFT(Complex[] fft, int index) {
    return fft[index].Magnitude * 2 / fft.Length;
}

Из формулы следует, что нулевому элементу соответствует частота 0 Гц. Такая странная частота может быть только у сигнала, в котором вообще нет колебаний (его осциллограмма выглядит как ровная горизонтальная линия). Эту часть сигнала называют постоянной составляющей, по английски DC offset [6].

Давайте уже перейдем к данным, графикам и картинкам.

Я сделал FFT преобразование первой секунды моего файла (длительность в 1 секунду примечательна тем, что в результирующем массиве индексы будут точно соответствовать значениям частоты). Рассмотрим первые 1000 элементов.

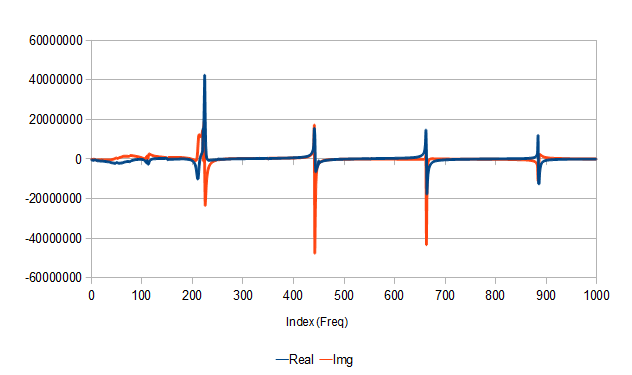
Элементы FFT на графике (вещественная и мнимая часть):

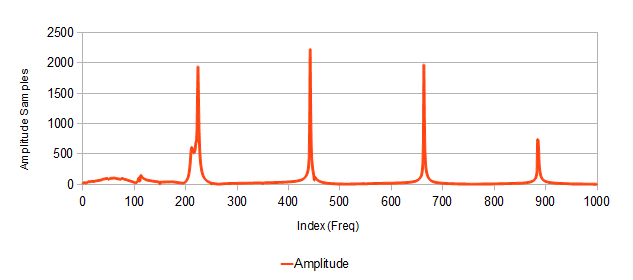
Амплитуда:

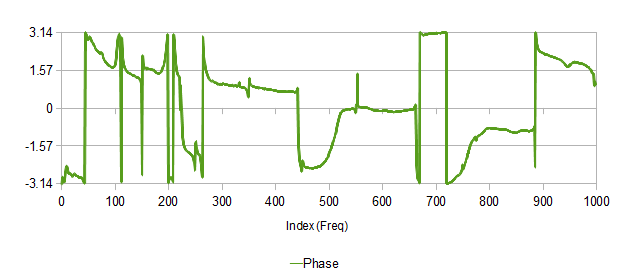
Фаза:

Обсудим полученные результаты.

График фазы получился чудным. В силу зацикленности этого показателя в пределах [-π, π] кривая рвется — там где значение выходит за вертикальные пределы, линия продолжается с противоположного края. Наверно, надо было использовать какой-то особый тип диаграммы, но не знаю какой.

Фаза частоты показывает, с каким смещением элементарная синусоида присутствует в сигнале. “Возмущения” наблюдаются на пиках амплитуды, а также в местах, где был вырезан шум электросети (50, 150, 250 Гц и т.д.)

Пики амплитуды соответствуют частотам основного тона (нота “ля”, 220 Гц) и его обертонов.

Интересно, что основной тон размазан на два пика: маленький на 212 Гц и большой на 224. Однако обертоны (пики точно на 442, 663 и 884 Гц) намекают на то, что частота должна была бы быть 221 Гц (ля + 4 цента).

Откуда взялась эта расстройка? Точно сказать не могу, но скорее всего вызвана деформацией струны при звукоизвлечении (щипке пальцем или ударе медиатором). Если вы пользовались цифровым тюнером для настройки гитары, то наверняка замечали, что сначала звук “плавает”, а спустя секунду стабилизируется. Так что это неотъемлемая фишка гитарного звука, и ее надо иметь в виду. Чем обусловлено повышение основного тона в целом на пару герц — не приложу ума, видимо тоже фишка.

Маленький пик в районе 113 Гц — это, скорее всего, резонирование открытой 5 струны, его можно проигнорировать. А возвышенность на нижних частотах — это колебания корпуса гитары.

Динамика изменения амплитуд

Интересно посмотреть, как эволюционирует громкость разных гармоник (да и негармонических составляющих). Для этого надо сделать спектрограммы нескольких коротких фрагментов на разных участках временной оси, снять амплитуды пиков и изобразить на графике.

Следующая функция на C# поможет мне автоматизировать процесс:

class StatItem {
    public int Freq;
    public long Time;
    public double Amplitude;
}

static IList<StatItem> CalculateFreqStats(string pcmFilePath, IEnumerable<int> frequences, IEnumerable<long> positions) {
    const int FFT_SIZE = 4410;
    var list = new List<StatItem>();

    foreach(var pos in positions) {
        var pcm = LoadPcm(pcmFilePath, pos - FFT_SIZE / 2, FFT_SIZE);
        var fft = CalculateFFT(pcm);
        foreach(var freq in frequences) {
            list.Add(new StatItem {
                Freq = freq,
                Time = pos,
                Amplitude = AmplitudeFromFFT(fft, IndexForFreq(fft, freq))
            });
        }
    }

    return list.OrderBy(t => t.Freq).ThenBy(t => t.Time).ToList();
}

Как видите, я зафиксировал FFT_SIZE на 4410. Это значит, что я смогу различать частоты с шагом 10 Гц, поэтому незначительной расстройкой относительно чистого “ля” можно пренебречь.

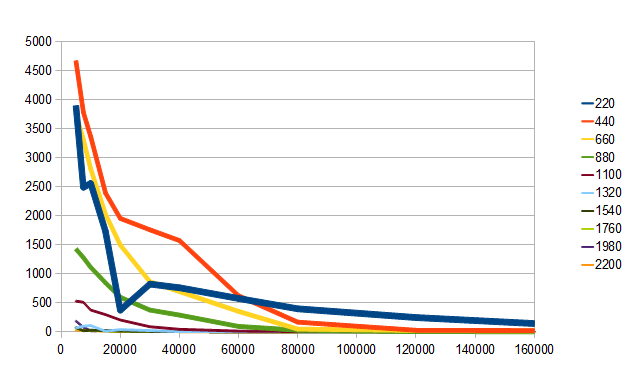
Вот 10 гармоник на одном графике (сравните с осциллограммой в самом начале статьи):

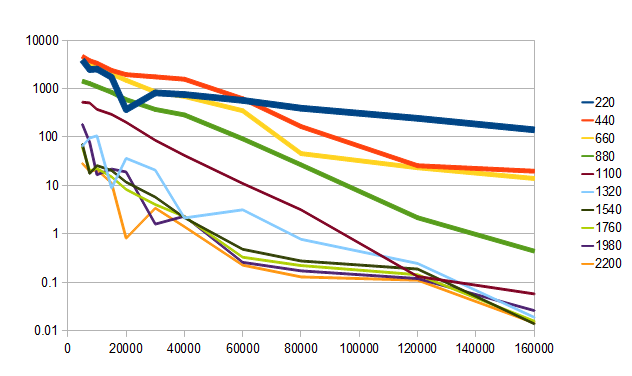
Тот же график с логарифмической вертикальной шкалой:

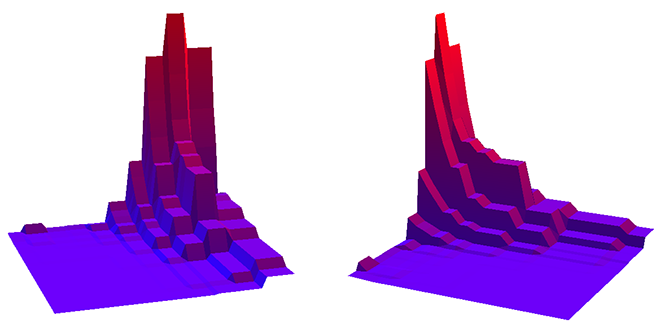
И даже в 3D:

Ну, тут есть о чем поговорить!

Видно, что все гармоники в целом экспоненциально затухают со временем, но некоторые из них при этом замысловато “колбасятся”.

Основной тон имеет резкий спад, но самый длинный “сустейн”. На протяжении первых полутора секунд доминирует вторая гармоника (уж не поэтому ли гитарные ноты записываются на октаву выше актуального звучания?!)

Соберу еще статистику по негармонической частоте 210:

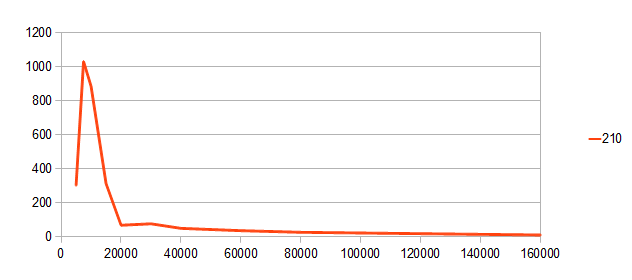
Здесь картина отличается: звук появляется и затухает в течение половины секунды.

Моделирование динамики амплитуд

Теперь, когда я собрал статистику амплитуды, я буду искать функцию, которая могла бы её смоделировать. Эксперименты с NonlinearFit в Maple показали, что наиболее адекватно кривые приближаются выражением:

$$ y = (Ax^2 + Bx + C) \cdot e^{Dx} $$

Наличие экспоненты диктуется формой графиков, а полином я добавил для симуляции “помятости”. Повышение степени многочлена, а также попытки использовать периодические синусы-косинусы ни к чему хорошему не привели.

Взгляните на интерполяции для некоторых гармоник:

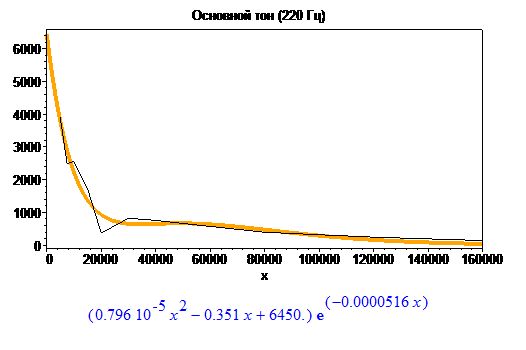
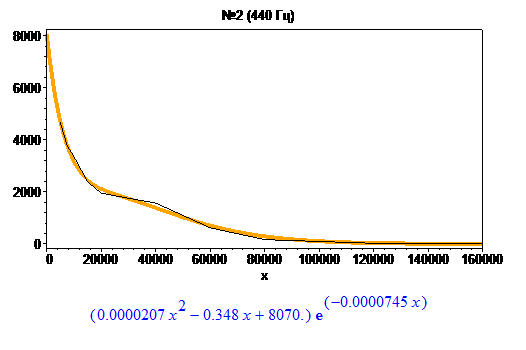
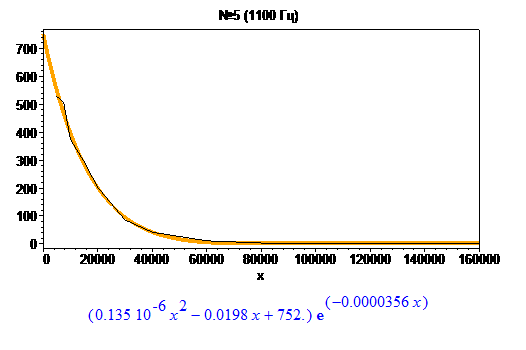
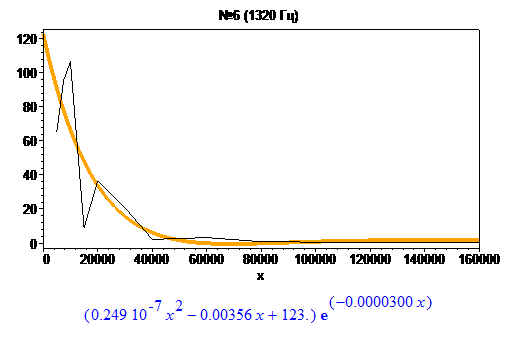
Значения коэффициентов собраны в таблицу:

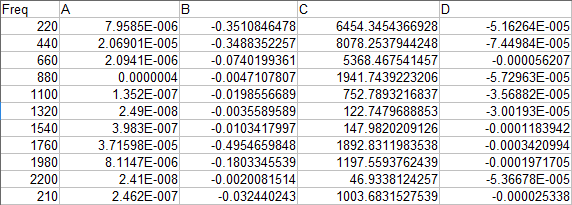
Ре-синтез!

Все готово для того, чтобы попробовать синтезировать гитарный звук программно, C# мне в помощь.

Понадобится вспомогательный класс для моделирования амплитуд:

class AmplitudeModel {
    double A, B, C, D;
    public AmplitudeModel(double a, double b, double c, double d) {
        A = a; B = b; C = c; D = d;
    }

    public double Calc(double time) {
        return (A * time * time + B * time + C) * Math.Exp(D * time);
    }
}

а также функция для генерирования чистых тонов:

static double CalcSine(double freq, double timeSample) {
    return Math.Sin(2 * Math.PI * freq * timeSample / SAMPLE_RATE);
}

Собственно функция генерации звука:

static short[] Synth(double baseFreq, double seconds) {
    var harmAmplitudeModels = new[] {
        new AmplitudeModel(0.0000079585,-0.3510846478,6454.3454366928,-0.0000516264),
        new AmplitudeModel(0.0000206901,-0.3488352257,8078.2537944248,-0.0000744984),
        new AmplitudeModel(0.0000020941,-0.0740199361,5368.4675414570,-0.0000562070),
        new AmplitudeModel(0.0000004000,-0.0047107807,1941.7439223206,-0.0000572963),
        new AmplitudeModel(0.0000001352,-0.0198556689,752.7893216837,-0.0000356882),
        new AmplitudeModel(0.0000000249,-0.0035589589,122.7479688853,-0.0000300193),
        new AmplitudeModel(0.0000003983,-0.0103417997,147.9820209126,-0.0001183942),
        new AmplitudeModel(0.0000371598,-0.4954659848,1892.8311983538,-0.0003420994),
        new AmplitudeModel(0.0000081147,-0.1803345539,1197.5593762439,-0.0001971705),
        new AmplitudeModel(0.0000000241,-0.0020081514,46.9338124257,-0.0000536678)
    };

    var inharmAmplitudeModels = new[] {
        new {
            FreqShift = -9,
            Strenght = 0.3,
            Model = new AmplitudeModel(0.0000002462,-0.0324402430,1003.6831527539,-0.0000253380)
        }
    };

    var sampleCount = Convert.ToInt32(seconds * SAMPLE_RATE);
    var result = new short[sampleCount];

    for(var timeSample = 0; timeSample < sampleCount; timeSample++) {
        double amplitudeSample = 0;

        for(var harmIndex = 0; harmIndex < harmAmplitudeModels.Length; harmIndex++) {
            var freq = baseFreq * (1 + harmIndex);

            // slight detune the main tone
            if(harmIndex == 0)
                freq += 2;

            amplitudeSample += harmAmplitudeModels[harmIndex].Calc(timeSample) * CalcSine(freq, timeSample);
        }

        foreach(var info in inharmAmplitudeModels) {
            var freq = baseFreq + info.FreqShift;
            amplitudeSample += info.Strenght * info.Model.Calc(timeSample) * CalcSine(freq, timeSample);
        }

        result[timeSample] = Convert.ToInt16(Math.Round(amplitudeSample));
    }

    return result;
}

Что здесь вкратце происходит: для заданной базовой частоты (ноты) я складываю 10 чистых синусоидальных сигналов (тон + 9 обертонов), умноженных на смоделированную функцию амплитуды. Собственно, это и есть аддитивный синтез [7].

Кроме того, есть две фишки: подмешивается сигнал на 9 Гц ниже основного тона (inharmAmplitudeModels), а сам основной тон расстраивается на 2 Гц вверх. Как оказалось, эти расстройки очень важны!

Будем слушать?

Вот синтезированная басовая нота “ми” (E2):

А это “соль” (G3):

А вот целая мелодия:

Та же мелодия с реверберацией и компрессором:

Заметили, как “по-настоящему” звучит концовка!? Звук получился похожим на clean electric guitar. Выраженные 2, 3 и 4 гармоники делают его даже, не побоюсь этого слова, “ламповым”.

Короче, я оцениваю результат как “успех”.

Дальнейшее развитие идеи

Может быть, вы обратили внимание, что при синтезировании я никак не учитывал фазы гармоник. Мне стало интересно, несут ли они полезную информацию. Добавив фазу в функцию синтеза и прослушав результат, я отчетливо услышал, что стал ярче выражен щелчок, который в оригинальном звуке был от удара по струне:

Другое направление возможного улучшения — это синтез по большему количеству обертонов, что особенно актуально для низких нот (потому что их обертоны имеют меньший шаг и большее их количество умещается в слышимый спектр).

Имеет смысл более точно моделировать огибающие амплитуд какими-нибудь сплайнами, а не обычной функцией, как сделал я.

Кроме того, коэффициенты моделей должны меняться от струны к струне и зависеть от силы удара, от лада, на котором струна зажата, и от позиции звукоизвлечения. Это тоже можно анализировать и пытаться обобщать,.. но мне самое время закруглиться и закончить статью. До свиданья!