Толстые хвосты
Эта статья — Jupyter-блокнот, в котором я пытаюсь обобщить текущий уровень моего понимания статистических распределений с толстыми хвостами, популярно описанных у Нассима Талеба и Бенуа Мандельброта.
Загрузим хитро подготовленные данные:
import numpy as np
data = np.loadtxt('data/fat-tails.tsv')
И посмотрим на гистограмму:
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = (8, 2)
plt.rcParams['figure.dpi'] = 144
def plot_hist():
plt.hist(data, bins=35, density=True, color='silver')
plt.figure()
plot_hist()
plt.show()
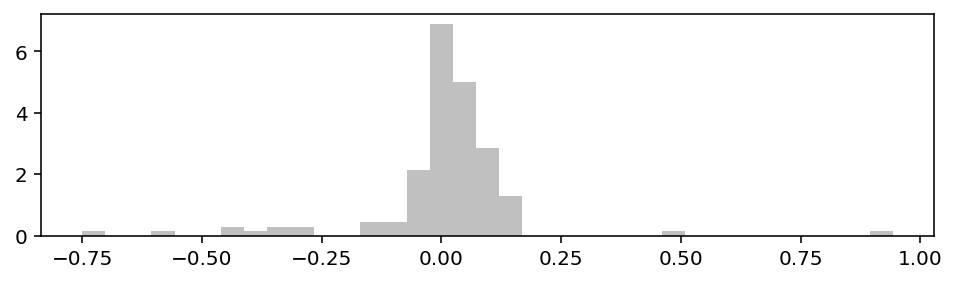
Ходят неподтверждённые слухи, что большинство людей, если видят подобный холм, сразу хотят натянуть на него нормальное распределение. Давайте и мы начнём с такого упражнения.
Проверка на нормальность
Первая идея — вычислить эмпирические параметры (mean, stdev) и нарисовать поверх гистограммы соответствующую кривую Гаусса:
m = np.mean(data)
sd = np.std(data, ddof=1)
m, sd
(0.006291666666666666, 0.1576599809096131)
import scipy.stats as stats
data_norm = stats.norm(m, sd)
def plot_pdf(dist, xmin, xmax, mirror=False, **kwargs):
x_list = np.linspace(xmin, xmax, num=250)
y_list = [dist.pdf(x) for x in x_list]
if mirror:
x_list = -x_list
plt.plot(x_list, y_list, **kwargs)
plt.figure()
plot_hist()
plot_pdf(data_norm, -1, 1, color='brown')
plt.show()
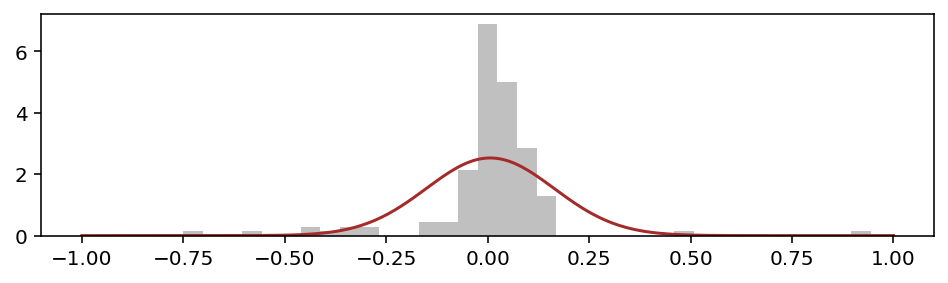
Не вписывается колокольчик. В пике кривая сильно недобирает, а плечи излишне широкие.
Геометрию такой гистограммы описывают словом leptokurtic, что означает высокий kurtosis. Для нормальных данных эта мера должна находиться в окрестности нуля, а у нас:
stats.kurtosis(data, fisher=True, bias=False)
13.912272835981184
Другая распространённая эвристика — правило трёх сигм. Почти все значения нормально распределённой величины умещаются в интервале μ ± 3σ. Проверим:
for k in [3, 4, 5]:
print('>', k, ':', [i for i in data if i < m-k*sd or i > m+k*sd])
> 3 : [0.944, -0.751, -0.574, 0.507]
> 4 : [0.944, -0.751]
> 5 : [0.944]
Известный критик нормального распределения Нассим Талеб в своём сборнике технических статей Statistical Consequences of Fat Tails на странице 55 пишет:
The heuristic is to reject Gaussianity in the presence of any event > 4 or > 5 STDs
Впрочем, есть и более формальные тесты, например D’Agostino K²:
stats.normaltest(data)
NormaltestResult(statistic=44.25984103909377, pvalue=2.4496138757306153e-10)
Близкое к нулю p-value указывает, что следует отвергнуть гипотезу о нормальном распределении.
Можно ли описать эти данные каким-то другим, более подходящим законом?
Lévy α-stable distributions
Есть одно интересное семейство распределений — stable distributions. Их ещё называют Lévy-stable, L-stable или α-stable.
Поль Леви разработал их теорию в первой половине XX века, а позже, в середине 60-х Бенуа Мандельброт нашёл им практическое применение, в частности, для описания колебаний рыночных цен.
Выборочно процитирую из книги (Не)послушные рынки:
Леви занялся теорией вероятностей, когда ему было уже под сорок. Вскоре после Первой мировой его попросили прочесть курс лекций о точности прицельной артиллерийской стрельбы. Это подтолкнуло его к выполнению самобытной научной работы; начал он с неудачно названных им “устойчивыми” вероятностных распределений.
Я назвал их “L-устойчивыми” в честь — а позднее и в память — Поля Леви.
Прикладной математики Леви всегда избегал. Когда я начал изучать распределение доходов, мне пришло в голову, что эти математические игры могут и пользу ещё принести: альфа и все другие элементы теории устойчивого распределения станут удобными инструментами для анализа реального мира. Так и получилось, о чём я написал в нескольких статьях о распределении личных доходов.
Когда я позже рассказал Леви о том, как развил его идеи и применил их к экономике, он поразился и, возможно, даже рассердился. По его мнению, “настоящие” математики просто не занимаются такими прозаическими вещами, как личные доходы или цены на хло́пок.
Удобная особенность этих законов распределения — 4 параметра, регулирующие все аспекты формы графика, что позволяет хорошо приспосабливаться к эмпирическим данным.
А главная проблема — вычислительная сложность. Нет явных формул ни для чего, кроме характеристической функции. Операция fit (подбор параметров) считает сложные интегралы, что занимает время. Но наберёмся терпения и выполним её на нашем массиве:
data_levy_stable_params = stats.levy_stable.fit(data)
print(data_levy_stable_params)
(1.3006854900338793, -0.8515766942972418, -0.04370014688443574, 0.0490248901910795)
Порядок параметров такой:
- α — ключевой параметр “альфа”, заслуживает отдельного описания ниже
- β — асимметрия (но не в классическом понимании)
- сдвиг — совпадает с мат-ожиданием
- масштаб — не является мерой дисперсии, ниже расскажу почему
А вот график:
data_levy_stable = stats.levy_stable(*data_levy_stable_params)
def plot_norm_and_levy_stable_combo():
plot_hist()
plot_pdf(data_norm, -1, 1, color='brown')
plot_pdf(data_levy_stable, -1, 1, color='g')
plt.figure()
plot_norm_and_levy_stable_combo()
plt.show()
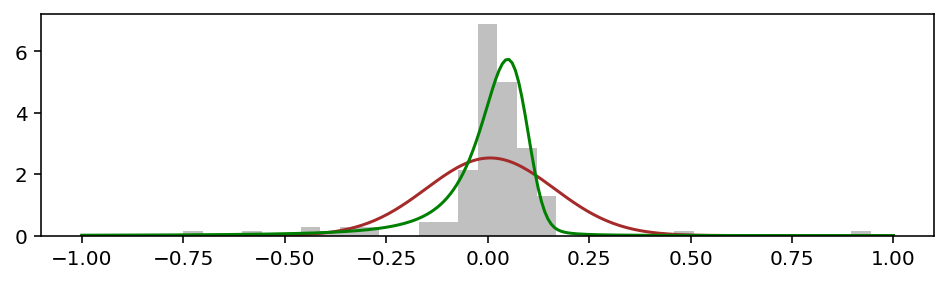
Видно, что зелёная кривая лучше подобралась к гистограмме и по высоте, и по ширине. Но более важное отличие — по краям, в так называемых хвостах, которые лучше видно в логарифмическом масштабе:
plt.figure()
plot_norm_and_levy_stable_combo()
plt.yscale('log')
plt.show()
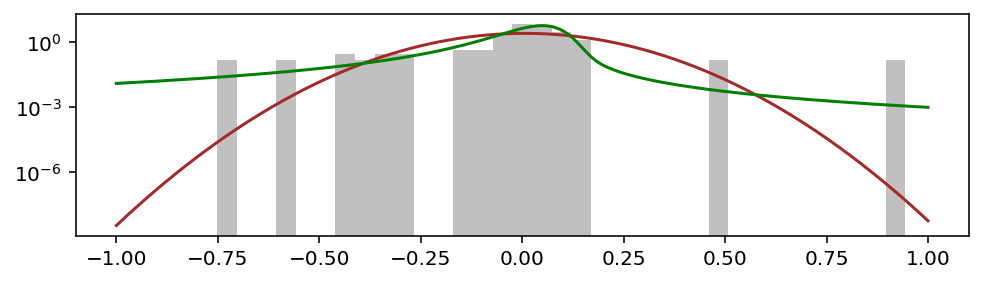
Главное — хвост!
Важность хвостов в том, что они описывают затухание вероятности больших отклонений. Там где красная кривая нормального распределения устремляется вниз, зелёная кривая stable-распределения идёт вбок, размазывая вероятность по горизонтальной оси. Такие хвосты называют толстыми (fat tails).
Параметр α — хвостовой индекс
alpha = data_levy_stable_params[0]
print(alpha)
1.3006854900338793
Выше я назвал параметр α ключевым, потому что именно он отвечает за “толщину” хвостов. Его значения варьируются в диапазоне от 0 до 2. Чем ближе к 2, тем ближе распределение к нормальному.
plt.figure()
for a in [1.5, 1.9, 1.99, 1.9999]:
plot_pdf(
stats.levy_stable(a, 0, 0, 0.125), -1, 1,
color='b', linewidth=a
)
plot_pdf(
stats.levy_stable(2, 0, 0, 0.125), -1, 1,
color='brown', linewidth=8, alpha=0.5
)
plt.yscale('log')
plt.show()
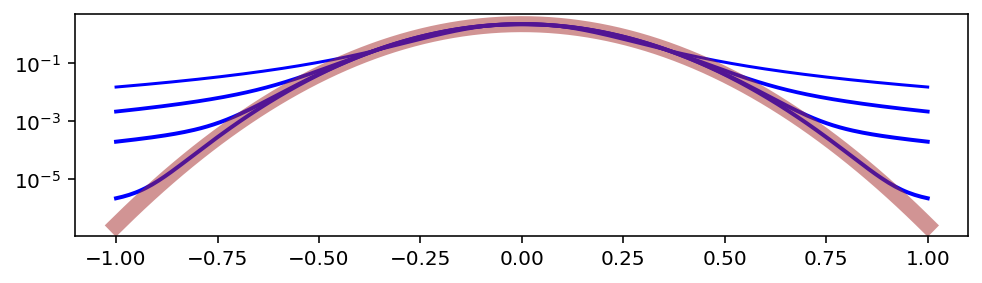
По мере удаления от пика, хвосты превращаются в распределение Парето, то есть в степенной закон с показателем степени α:
plt.figure()
plot_pdf(
stats.pareto(alpha, 0, 0.00395), 0.1, 2,
color='y', linewidth=8, alpha=0.5
)
plot_pdf(
stats.pareto(alpha, 0, 0.028), 0.1, 2, mirror=True,
color='y', linewidth=8, alpha=0.5
)
plot_pdf(data_levy_stable, -2, 2, color='g')
plt.yscale('log')
plt.show()
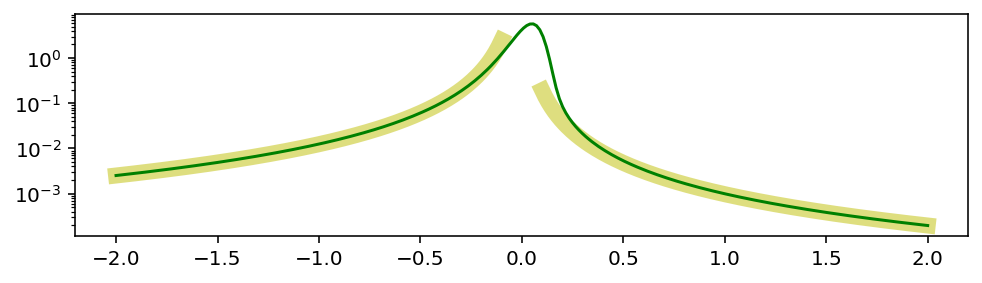
Степенные законы — отдельная интересная тема, связанная с такими понятиями как масштабная инвариантность и фракталы. Ах вот причём тут Мандельброт… или всё наоборот?
Важная особенность степенных законов: существование математического ожидания, дисперсии и других моментов зависит от α. Например, дисперсия не определена при α ⩽ 2, потому что в её формуле (α - 2) в знаменателе.
Если α ⩽ 1, то нет даже математического ожидания. Для таких данных невозможна никакая статистика, а прогнозирование сводится к “может быть что угодно”.
Закон больших чисел работает медленно
В этом несложно убедиться экспериментально:
def plot_LLN(n: int, dist, color):
samples = dist.rvs(size=n)
x = []
y = []
for i in range(1, n):
x.append(i)
y.append(np.mean(samples[0:i]))
plt.axhline(dist.mean(), color=color, linestyle='--')
plt.plot(x, y, color=color)
np.random.seed(seed=12345+13) # 11 13 15 20 21
plt.figure()
plot_LLN(100_000, data_levy_stable, 'g')
plot_LLN(100_000, data_norm, 'brown')
plt.show()
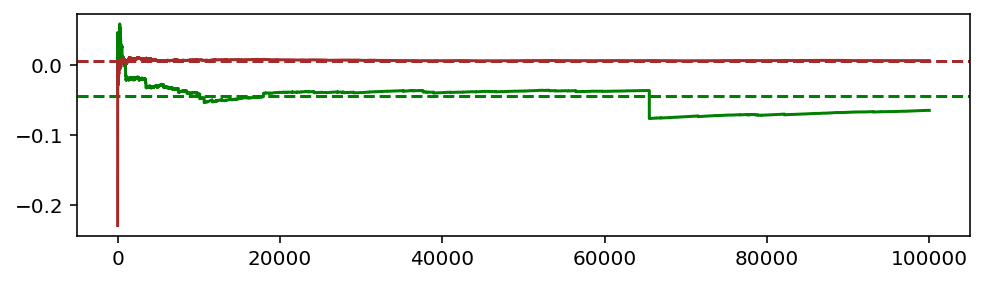
Пунктирная линия — истинное математическое ожидание. Сплошная — последовательные приближения, полученные усреднением нарастающего массива сгенерированных случайных чисел.
Для нормального распределения (красный цвет) быстро происходит стабилизация, и эмпирическое значение более не отрывается от теоретической линии. На этом фундаменте стоит вся статистика.
В зелёном графике для stable-распределения видны артефакты:
- Медленное приближение к пунктирной линии.
- Умеренные флуктуации.
- Резкий скачок, вызванный так называемым чёрным лебедем (редким значением, сильно отличающимся от среднего).
Теперь понятно, почему Мандельброт посчитал название “устойчивые” неудачным.
Если мы попробуем начертить аналогичную диаграмму для α < 1, то получится вот что:
np.random.seed(seed=12345)
plt.figure()
plot_LLN(100_000, stats.levy_stable(0.6, 0, 0, 0.1), color='r')
plt.show()
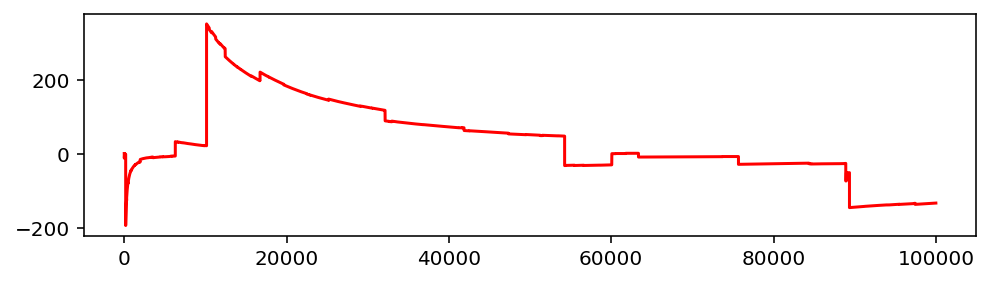
Сколько ни усредняй, стабильного значения не получится. Постоянно будут возникать отклонения, портящие всю накопленную статистику. Долина чёрных лебедей, так сказать.
Тогда как работает функция fit?
Подгонка параметров делается методами максимального правдоподобия, которые по сути являются оптимизационными процедурами и не опираются на закон больших чисел.
Талеб одобряет (Consequences, page 34):
Consequence 7. Maximum likelihood methods can work well for some parameters of the distribution (good news).
Полученные таким образом оценки он называет “plug-in estimator”, а моменты получившегося распределения — shadow moments. Предлагается считать их предпочтительными, потому что они “схватывают” низкие вероятности, не реализовавшиеся в ограниченном объёме наблюдаемых данных.
Этот эффект мы видели на графике выше. Теперь сравним числа. Вот наблюдаемые (эмпирические) параметры:
print(f'Mean: {m:.2f}, Variance: {sd*sd:.2f}')
Mean: 0.01, Variance: 0.02
А вот shadow/plug-in значения, которые даёт подобранный закон распределения:
print(f'Mean: {data_levy_stable.mean():.2f}, Variance: {data_levy_stable.var()}')
Mean: -0.04, Variance: inf
Большая ли разница? Если это доходность в процентах годовых, то +1% против -4%.
Дисперсия бесконечна, потому что альфа меньше 2. Талеб агитирует вместо неё использовать mean absolute deviation.
Если интересен только хвост
Представим теперь, что мы нидерландские учёные (ха-ха), и надо рассчитать высоту дамбы, которая защитит от следующего наводнения. Из истории прошлых лет мы хотим сделать вывод о необходимой высоте плотины.
В таких случаях интерес представляет только правый хвост распределения, к которому можно пытаться прилаживать непосредственно степенной закон. В самых общих словах это то, чем занимается направление статистики под названием extreme value theory. Вот плейлист по теме.
Воспользуемся пакетом powerlaw, который судя по документации точно создали люди от науки.
import powerlaw
powerlaw_fit = powerlaw.Fit([i for i in data if i > 0])
print('alpha:', powerlaw_fit.power_law.alpha)
Calculating best minimal value for power law fit
alpha: 2.445934502535503
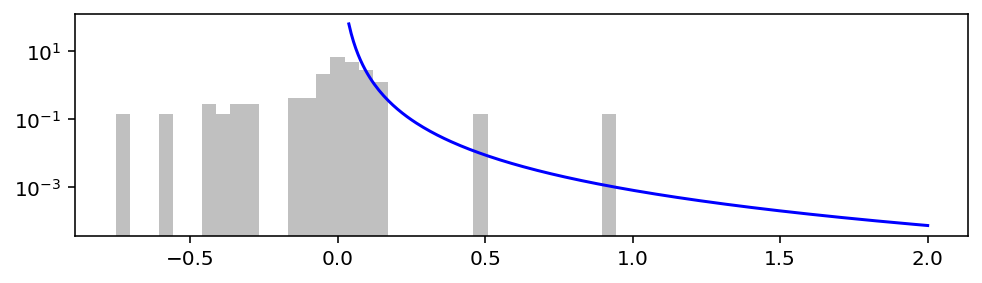
Для правой части получилось α = 2.45.
Да, в отличие от stable-распределения, у степенного закона α может быть любым. Но есть мнение, что полученные таким образом значения α завышены.
plt.figure()
plot_hist()
plot_pdf(
stats.pareto(powerlaw_fit.power_law.alpha, 0, powerlaw_fit.power_law.xmin),
powerlaw_fit.power_law.xmin, 2,
color='b'
)
plt.yscale('log')
plt.show()
Теперь всегда используем stable-распределения и степенные законы?
Об уместности их применения идут дискуссии:
- Are your data really Pareto distributed?
- No Stable Distributions in Finance, please!
- SFB 649 Discussion Paper 2005-008 (search for ’unfortunately’)
Также процитирую из Википедии:
Хотя степенной закон привлекателен по многим теоретическим причинам, доказательство того, что данные и в самом деле следуют степенному закону, требует больше, чем простого подбора параметров модели.
Я думаю, эти распределения можно использовать всегда, когда хочется перестраховаться. В худшем случае вероятность экстремальных отклонений будет завышена. И это не обязательно плохо. Ведь как гласит народная мудрость, лучше перебдеть.
Другая важная мысль, которую я предлагаю иметь в виду — не всегда по числовому ряду можно сделать статистические выводы. Бывает так, что даже среднее значение не имеет смысла.