blog.amartynov.ru

Теорему Котельникова я уже вскользь упоминал в статьях про интерполяцию и синтез гитарного звука. Сегодня чувствую в себе силы углубиться в тему по-полной, буквально нырнуть с головой.

Чтобы никого не обидеть, теорему эту называют теоремой Котельникова — Найквиста — Уиттакера — Шеннона, или попросту теоремой отсчётов (the Sampling theorem). Она считается одним из важнейших результатов теории информации.

Формулировка достаточно простая:

Если аналоговый сигнал не содержит в своем спектре частот выше Fmax, то его можно идеально точно восстановить по дискретным отсчётам, взятым равномерно с частотой строго большей 2·Fmax.

Даже если вы не имеете никакого отношения к обработке сигналов, очень может быть, что вам знакома фраза “CD quality 44100 Hz”. Имеется в виду, что на компакт-дисках звук хранится в виде дискретных отсчётов, по 44100 штук на секунду. А это, согласно озвученной теореме, означает что “на CD можно идеально записать звук с частотой до 22050 Гц”, что вполне себе хорошо, так как слышимый человеком диапазон укладывается в эти рамки.

Казалось бы, всё отлично, что тут ещё обсуждать. Но у меня возник ряд вопросов:

1. Ограниченность по частоте — так ли это просто, как кажется на первый взгляд?

2. Как именно предполагается восстанавливать сигнал, чтобы получилось “идеально точно”?

3. Что будет, если в оцифровываемом сигнале окажутся частоты равные или превосходящие допустимую половину частоты дискретизации? Они проигнорируются, или произойдет что-то другое?

В процессе поиска ответов я углублялся в детали, а оттуда сверкал глазами скрывающийся в них дьявол.

Должен предупредить, будет много страшной математики…

Финитность и ограниченность

Сперва хотел обойтись без специальных терминов, но не получилось. Для дальнейших рассуждений понадобятся два определения:

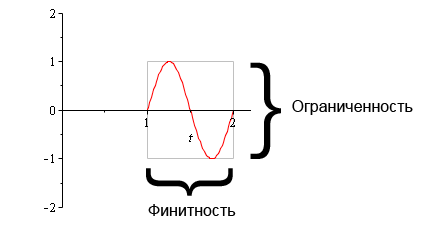
Финитность означает, что функцию можно заключить в горизонтальные рамки. Ограниченность — в вертикальные. Вместо “финитная функция” часто говорят “функция с компактным носителем”.

Закрепим на примерах:

Большинство обычных функций, с которыми мы имели дело ещё в школе, не являются ни финитными, ни ограниченными.

Синус и косинус — не финитные, но ограниченные.

Примером финитной, но не ограниченной функции может служить функция Дирака, с которой мы столкнемся совсем скоро.

Финитными и ограниченными одновременно являются, в основном, кусочные функции — например, сплайны, вейвлеты.

В формулировке теоремы теперь можно заменить фразу “сигнал не содержит частот выше такой-то” более умным выражением: “преобразование Фурье сигнала является финитной функцией”.

Всё поняли? Тогда едем дальше.

Бесконечный сигнал в вакууме

Возьмем для изучения синусоидальный сигнал частоты 1 Гц:

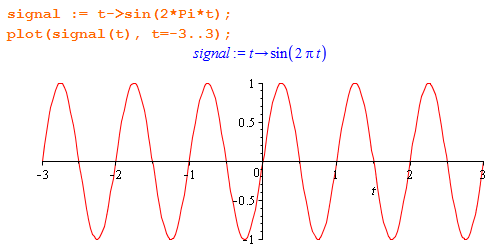
Это не финитный сигнал — он простирается влево и вправо как минимум до тех пор, пока шпалы не закончатся. Посмотрим на его спектр:

На графике пусто, и это неудивительно, потому что его невозможно нарисовать: он всюду ноль, кроме точки 1, в которой уходит в бесконечность. Я же обещал функцию Дирака? Вот это она и есть.

В принципе, всё логично: сигнал содержит ровно одну частоту и бесконечно длится, значит содержит бесконечное количество энергии, поэтому в его спектре тоже должна где-то быть бесконечность. Такую радикальную форму принимает закон сохранения.

Спектр отличен от нуля лишь в одной точке, значит он финитный и удовлетворяет теореме Котельникова. То есть, как бы это жутко не звучало, бесконечно длинную синусоиду можно идеально восстановить по бесконечному количеству дискретных значений.

Попробуем избавиться от бесконечностей.

Кусочек синуса

Я ограничу сигнал окном в 3 секунды:

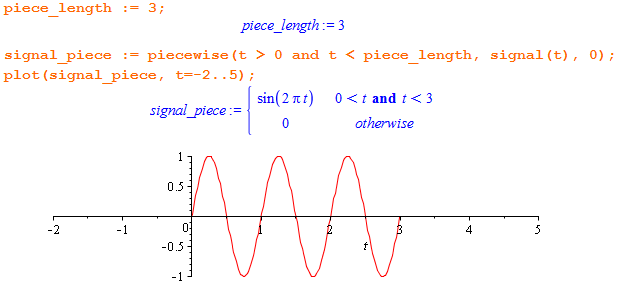
Теперь сигнал какой? Правильно — и финитный, и ограниченный. Что же с его спектром?

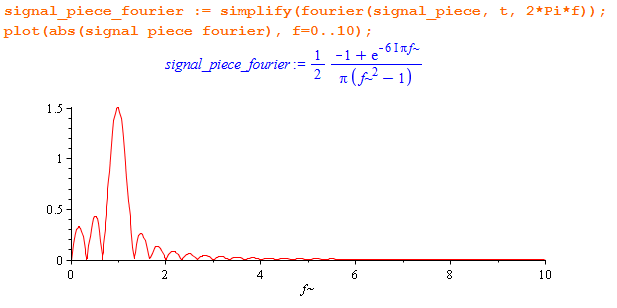
Как видите, Maple весьма крут, он смог вычислить преобразование Фурье для кусочной функции аналитически. И к большой (но преждевременной) радости оно больше не содержит никаких “дираков”, и его можно изобразить.

Из формулы и из картинки видно, что спектр стал ограниченным, но перестал быть финитным. Он растекся (произошел spectral leakage), справа и слева от основной частоты возникли так называемые “боковые лепестки”, которые уходят в бесконечность вправо.

Как же из одной единственной частоты мог возникнуть бесконечный спектр?!

Попробую объяснить это явление себе и вам. В двух точках, где я “обрубил” сигнал, возникли два перелома амплитуды — график перестал быть гладким. Но Фурье-преобразование рассматривает сигнал как сумму элементарных синусоид, в которой переломы можно “сэмулировать” только с помощью бесконечного числа синусов всех возможных частот.

Не верится? Тогда предлагаю следующий эксперимент. Послушайте несколько раз вот этот звук, состоящий из резко начинающихся и прекращающихся фрагментов синуса на частоте 500 Гц (похоже на сигнал “занято” в телефоне):

Отчетливо слышны щелчки или тупые постукивания! Перкуссионные звуки наше ухо слышит тогда, когда есть шумовой всплеск, то есть много разных частот в течение короткого промежутка времени.

Интуиция подсказывает, что для ослабления щелчков надо делать плавное нарастание и затухание сигнала (fade):

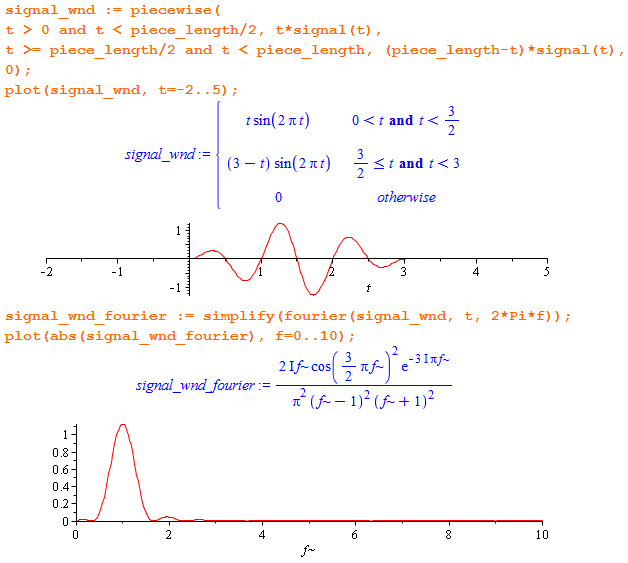
Это называется “применить к сигналу треугольное весовое окно”. В первой половине он линейно растет, во второй — линейно убывает.

Видно, что спектр почти прочистился от “лепестков”, но финитным так и не стал. И понятно почему — треугольное окно тоже нельзя представить конечной суммой синусов. Кроме того, “главный лепесток” разнесло вширь (ухудшилось разрешение по частоте).

Используя разные оконные функции (отдельная большая тема), можно лишь в некоторых пределах контролировать форму растекания спектра, но совсем избавиться от этого явления нельзя. Кроме того, применение окна — это всегда искажение амплитуды исходного сигнала.

Шэф! Всё пропало?

Оказывается, есть целая теорема Бенедикса о том, что функция не может быть финитной одновременно во времени и по частоте. То есть одно из двух — либо сигнал бесконечной длины, либо спектр бесконечной ширины. Так проявляется в обработке сигналов принцип неопределенности.

Неожиданно я получаю ответы на два первых вопроса:

1. Ни один реально существующий сигнал не удовлетворяет условиям теоремы Котельникова!

2. Нет способа идеально восстановить реальный сигнал по дискретным отсчётам!

Что ж, не бросать же дело на полпути. Давайте всё равно посмотрим, как теорема Котельникова отработает, хоть и при не выполненных условиях.

Дискретизация

Вернемся к 3-секундному фрагменту синуса. В нём была единственная интересная частота — 1 Гц.

Закроем глаза на то, что на самом деле спектр нефинитный и явно вылезает за пределы 1 Гц. Но будем об этом помнить, чтобы постараться не делать неверных выводов!

В свете вышесказанного решаем, что для оцифровки 1 Гц нужно взять отсчёты с частотой строго больше 2 Гц.

Чтобы числа получались попроще, я выбрал 3 Гц. На 3 секунды 9 отсчётов:

Вот как они выглядят на графике:

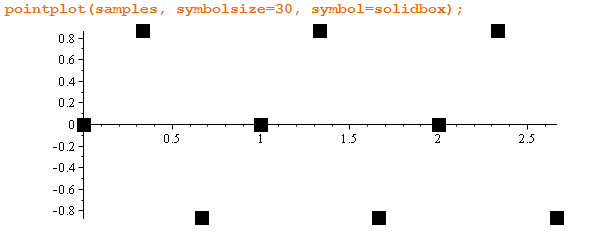
Теперь, чтобы восстановить непрерывный сигнал по отдельным точкам, нужно применить какую-нибудь интерполяцию.

Интерполяция ступеньками

Самый простой способ — это интерполяция ступенчатой функцией (zero-order hold):

Форма волны исказилась очень сильно (оквадратилась):

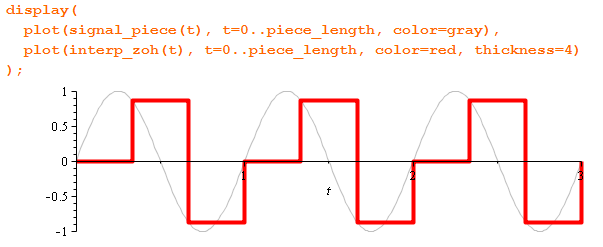
А со спектром произошли более интересные приключения:

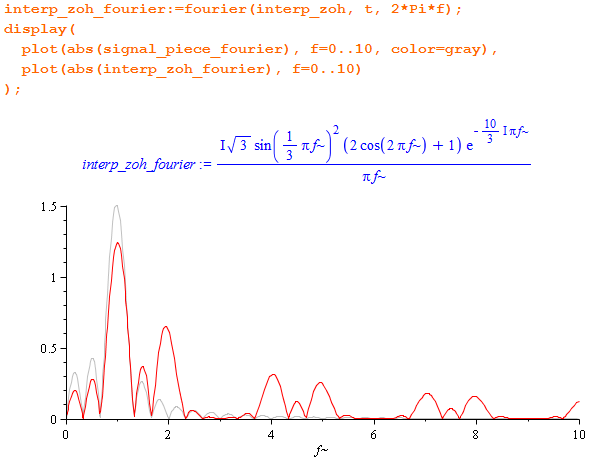
На полезном диапазоне (в районе 1 Гц) форма спектра примерно соответствует оригинальному сигналу, только чуть “тише”. А справа видим вспучивания на определенных частотах: загадочный пик 2 Гц и уходящие в бесконечность периодические реплики. В сигнале возник высокочастотный мусор.

Продолжим.

Линейная интерполяция

Можно вычислять значения сигнала по двум соседним точкам, это будет линейная интерполяция (или first-order hold):

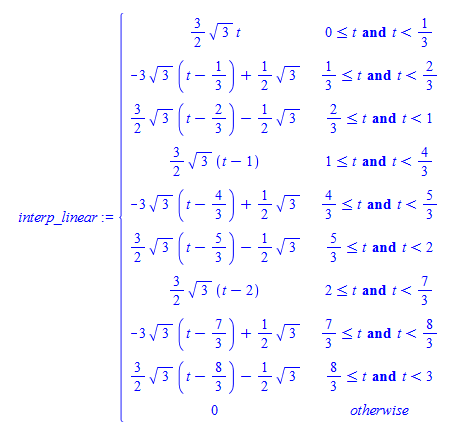
Восстановленный зубастый сигнал:

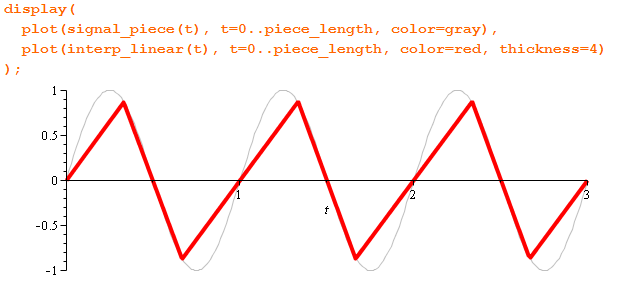
Спектр:

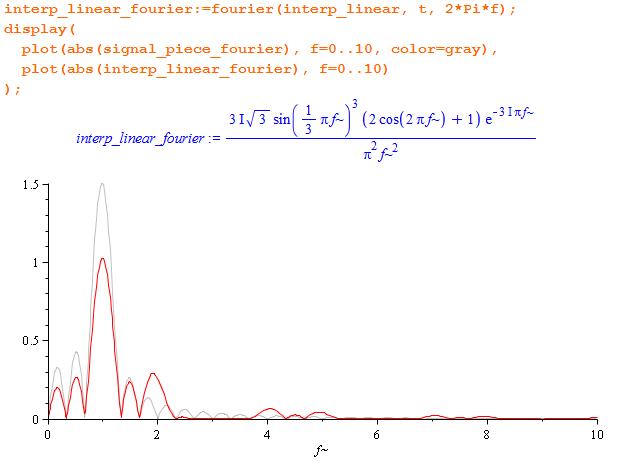
В принципе, картина похожа, но мусора стало поменьше.

А дают ли авторы теоремы рецепт восстановления? Конечно дают!

Интерполяция sinc-функциями

Формула идеального восстановления сигнала “идёт в комплекте” с теоремой:

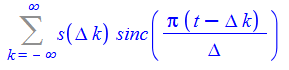
Здесь sinc — это ненормированный кардинальный синус:

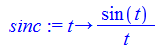
В случае конечного числа отсчётов бесконечную сумму вполне можно посчитать. Посмотрим, что получится из моих 9 точек:

Спектр:

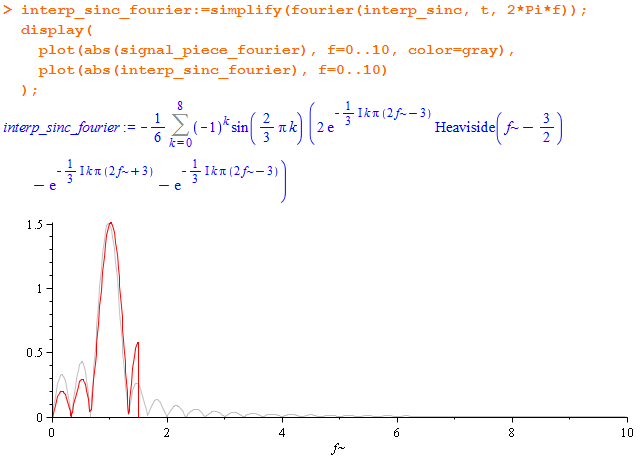
Смотрите, форма восстановленного сигнала максимально приближена к оригиналу — это хорошо. То что он расползся, не является большой проблемой — нас не очень интересует поведение за пределами интервала 0 < t < 3.

В спектре хорошо заметен обрыв ровно на половине частоты дискретизации — высокочастотных “добавок” нет. Но в полезном диапазоне искажения всё же присутствуют. И это неудивительно — мы же помним, что идём напролом, применяя теорему к нефинитному по частоте сигналу.

Какую интерполяцию использовать?

Выше я попробовал три типа интерполяции, которые (если уж совсем вдаваться в детали) являются одной и той же интерполяцией полиномами Лагранжа только с разным числом равноудалённых узлов.

Sinc-ряд — предельный случай, когда задействовано бесконечное количество дискретных значений (подробности).

Чем больше отсчётов используется, тем более гладким и близким к оригиналу получается восстановленный сигнал. Но за это приходится платить. Если ступенчатую интерполяцию реализовать очень просто (всего-то надо менять выходное значение с каждым новым поступившим сэмплом), то sinc-интерполяция с вычислительной точки зрения весьма сложна.

Sinc-ряд можно применять для высококачественной оффлайновой обработки на компьютере. А вот в таких устройствах как, например, цифро-аналоговый преобразователь звуковой карты, такая роскошь может быть недоступна.

Было хорошо видно, что локальная интерполяция по ограниченному числу точек добавляет в выходной сигнал высокочастотные компоненты в виде затухающих периодических копий полезной полосы частот. В англоязычных источниках эти артефакты называют словом “imaging”.

Возникают они из-за того, что финитные интерполяторы (прямоугольники в случае zero-order hold и треугольники в случае линейной интерополяции) имеют нефинитные спектры.

Для удаления высокочастотного мусора результат любой не-sinc интерполяции необходимо пропускать через фильтр нижних частот, так называемый реконструкционный фильтр. В аппаратных устройствах это будет аналоговый фильтр (который делается из катушек и конденсаторов), при программном upsampling-е — цифровой.

Что если оригинал содержит частоты выше или равные половине частоты дискретизации?

Внесём изменение в исходный эксперимент — удвоим частоту изучаемого сигнала. Теперь 3 Гц окажется заведомо недостаточно (3 < 2·2), и вот как это скажется на восстановленном сигнале:

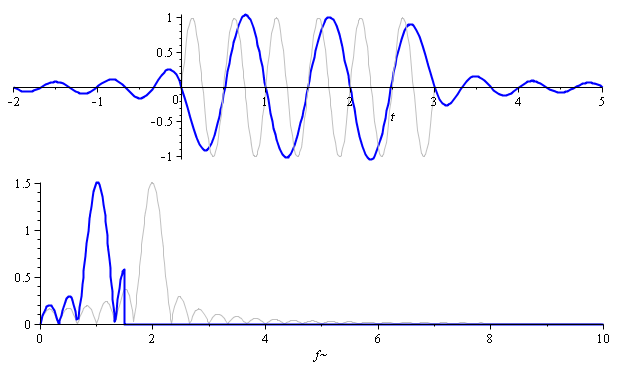
На спектрограмме отлично видно, как частота восстановленного сигнала отразилась от половины частоты дискретизации. Она не проигнорировалась, а запечатлелась в искаженном виде.

Очень важно это знать! Например, при записи звука высокочастотные помехи от мобильников и других устройств могут попасть в запись.

Это явление называется алиасингом (aliasing). Термин подходит очень точно: у высокочастотных компонентов сигнала появляются “двойники”, “алиасы” в области низких частот.

Если частота дискретизации точно равна удвоенной частоте сигнала, то возникают чудеса другого характера. Например, вот отсчёты, получившиеся при оцифровке сигнала 1 Гц с частотой 2 Гц:

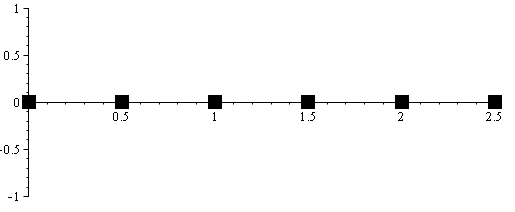
Одни нули, потому что замеры попали на те точки, где синус равен нулю. Конечно, из такой информации сигнал восстановить не получится. Но если начать оцифровку с задержкой в четверть периода, то отсчёты попадут в пики — то есть тут как повезет.

Если даже совсем немного поднять частоту выборки (например, до 2.01 Гц), то сигнал начнет постепенно проявляться:

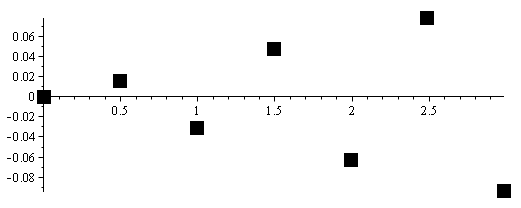
(возникающая при этом пульсация амплитуды отсчётов и сопутствующие недоразумения заслуживают отдельного обсуждения)

Именно алиасинг не позволил восстановить фрагмент синуса по дискретным отсчётам со 100% точностью. Высокочастотные компоненты, отражаясь, слегка модифицировали область низких частот.

Для реальных сигналов, которые, как мы теперь знаем, не удовлетворяют условиям теоремы Котельникова, полностью избавиться от алиасинга в строгом математическом смысле нельзя. Но его можно ослабить на необходимое число децибел с помощью фильтра нижних частот, подавляя часть спектра за пределами половины частоты дискретизации.

Такой фильтр, anti-aliasing filter, всегда применяют до оцифровки или до downsampling-а.

Фильтры и Oversampling

Как мы выяснили, НЧ-фильтры — незаменимый инструмент, совершенно необходимый как при дискретизации, так и при интерполяции сигналов.

Ирония жестокого мира заключается в том, что самый лучший, идеальный фильтр нижних частот — это sinc-фильтр, вычислять который так же сложно, как и sinc-интерполяцию (пример). Собственно, sinc-интерполяция — это и есть применение sinc-фильтра к дискретным отсчётам.

На практике приходится использовать более простые, но неидеальные фильтры, которые могут вносить те или иные искажения и всегда имеют так называемую полосу перехода между зонами пропускания и подавления частот (transition band). Ширину этой полосы необходимо знать и закладывать при оцифровке, чтобы с одной стороны максимально подавить алиасинг/imaging, а с другой — не ослабить полезную часть спектра. Так например, в Audio CD на полосу перехода отведено 2.05 кГц, что вообще-то не очень много.

Чем у́же полоса перехода, тем сложнее в реализации фильтр. В современных реалиях цифровые фильтры лучше, проще, дешевле и надёжнее, чем аналогичные аналоговые (простите за каламбур). Поэтому повсеместно применяется oversampling — трюк, заключающийся в использовании частоты дискретизации, в разы превышающей рекомендованную теоремой. В русском языке можно встретить названия “избыточная дискретизация” и “дискретизация с запасом”.

Как это работает?

Допустим нужно оцифровать звук, потолок — 20 кГц. В качестве частоты дискретизации возьмём не привычные 44.1 или 48, а, например, 100 кГц. Если так, то алиасинг будет начинаться на 50 кГц, и аналоговому антиалиасинговому фильтру будет где “развернуться” — 30 кГц на полосу перехода. На следующем шаге ужé цифровой сигнал подвергается downsampling-у с применением цифрового фильтра, для которого крутизна спада не является такой большой проблемой.

Восстановление сигнала идёт по обратной схеме:

• Upsampling с использованием цифрового фильтра.
• Простейшая интерполяция “ступеньками” в цифро-аналоговом преобразователе.
• Очистка полученного аналогового сигнала от мусора, возникшего на очень высоких частотах, относительно простым аналоговым фильтром.

Дополнительно, за счёт усреднения большего количества измерений oversampling позволяет увеличивать динамический диапазон и отношение сигнал-шум. С помощью него компания Philips уладила разногласия с Sony относительно битности компакт дисков (см. The history of the CD и Evolution of DAC & digital filter).

Выводы

Все выводы уже давно известны человечеству (точнее той его части, которая занимается обработкой сигналов). В данной статье я попытался донести их в удобной форме до тех, кто только изучает вопрос. Да и сам я в процессе написания текста и последовавших многочисленных правок лучше вник в материал.

Теорема Котельникова отвечает на вопрос, как часто нужно делать замеры, чтобы сохранить информацию обо всех “интересных” частотах, предупреждает о необходимости применения НЧ-фильтров и даёт рецепт восстановления сигнала с минимально возможными искажениями.

К сожалению, в реальной жизни нет ни сигналов с по-настоящему финитным спектром, ни идеальных фильтров, да и применить формулу sinc-интерполяции возможно далеко не всегда.

С другой стороны, реальные сигналы, с которыми мы имеем дело, тоже не идеальны: это всегда сигналы дискретного времени, а точность измерения амплитуды всегда ограничена уровнем шума и чувствительностью приборов. Как выглядит “оригинальный” сигнал, можно только догадываться, и абсолютно точное его воспроизведение невозможно и не нужно. Наоборот, некоторые специалисты считают основным преимуществом цифровых сигналов тот факт, что мы сами выбираем его поведение между отсчётами!